Sistem – Sistem Bilangan, Operasi dan kode
Tujuan Topik Bahasan
- Mengulas kembali sistem bilangan desimal.
- Menghitung dalam bentuk bilangan biner.
- Memindahkan dari bentuk bilangan desimal ke biner dan dalam biner ke dalam desimal.
- Penggunaan operasi aritmatika pada bilangan biner.
- Menentukan komplemen 1 dan 2 dari sebuah bilangan biner.
- Dan lain – lainnya……..
Sistem Bilangan
Sistem
Biner dan Kode – kode digital merupakan dasar untuk komputer dan
elektronika digital secara umum. Sistem bilangan biner seperti desimal,
hexadesimal dan oktal juga dibahas pada bagian ini. Operasi aritmatika
dengan bilangan biner akan dibahas untuk memberikan dasar pengertian
bagaimana komputer dan jenis – jenis perangkat digital lain bekerja.
Bilangan Desimal
Dalam setiap bilangan desimal terdiri dari 10 digit, 0 sampai dengan 9
Contoh:
- Ungkapkan bilangan desimal 2745.214 sebagai penjumlahan nilai setiap digit.
Bilangan Biner- Sistem Bilangan biner merupakan cara lain untuk melambangkan kuantitas, dimana 1 (HIGH) dan 0 (LOW).
- Sistem bilangan biner mempunyai nilai basis 2 dengan nilai setiap posisi dibagi dengan faktor 2:
Contoh :
Konversikan seluruh bilangan biner 1101101 ke desimal
- Sistem Bilangan biner merupakan cara lain untuk melambangkan kuantitas, dimana 1 (HIGH) dan 0 (LOW).
- Sistem bilangan biner mempunyai nilai basis 2 dengan nilai setiap posisi dibagi dengan faktor 2:
Contoh :
Konversikan seluruh bilangan biner 1101101 ke desimal
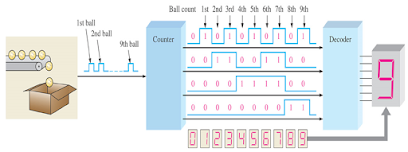
Aplikasi Digital
Ilustrasi sebuah penggunaan hitungan biner sederhana.
Konversi Desimal ke Biner
- Metode Sum-of-Weight.
- Pengulangan pembagian dengan Metode bilangan 2 (Repeated Division by 2 Method)
- A systematic method of converting whole numbers from decimal to binary is the repeated division-by-2 process.
- A systematic method of converting whole numbers from decimal to binary is the repeated division-by-2 process.
- Konversi fraksi desimal ke biner.
Binary Arithmetic
- Binary arithmetic is essential in all digital computers and in many other types of digital systems.
- Addition,Subtraction, Multiplication, and Division
Binary Addition
The four basic rules for adding binary digits (bits) are as follows:
0 + 0 = 0 sum of 0 with a carry of 0
0 + 1 = 1 sum of 1 with a carry 0f 0
1 + 0 = 1 sum of 1 with a carry of 0
1+ 1 = 10 sum of 0 with a carry 0f 1
Binary Subtraction
The four basic rules for subtracting bits are as follows:
0 – 0 = 0
1 – 1 = 0
1 – 0 = 1
10 – 1 = 1 0 – 1 with a borrow of 1
Binary Multiplication
The four basic rules for multiplying bits are as follows:
0 X 0 = 0
0 X 1 = 0
1 X 0 = 0
1 X 1 = 1
Binary Division
Division in binary follows the same procedure as division in decimal.
1’s and 2’s Complements of Binary Numbers
- The 1’s and 2’s Complements of Binary Numbers are very important because they permit the representation of negative numbers.
- The method of 2’s compliment arithmetic is commonly used in computers to handle negative numbers
Finding the 1’s Complement
The 1’s complement of a binary number is found by changing all 1s to 0s and all 0s to 1s.
Example:
1 0 1 1 0 0 1 0 (Binary Number)
0 1 0 0 1 1 0 1 (1’s Complement)
Finding the 2’s Complement
The 2’s complement of a binary number is found by adding 1 to the LSB of the 1’s complement
Alternative Method to find 2’s Complement
- Start at the right with the LSB and write the bits as they are up and including the first 1
- Take the 1’s complements of the remaining bits
Signed Numbers
Digital
systems, such as the computer, must be able to handle both positive and
negative numbers. A signed binary number consists of both sign and
magnitude information. The sign indicates whether a number is positive
or negative and the magnitude is the value of the number. There three
forms in which signed integer (whole) numbers can be represented in
binary:
⦁ Sign-Magnitude
⦁ 1’s Complement
⦁ 2’s Complement
The Sign Bit
The left-most bit in a signed binary number is the sign bit, which tells you whether the number is positive or negative.
Sign-Magnitude Form
When
a signed binary number is represented in sign-magnitude, the left-most
bit is the sign bit and the remaining bits are the magnitude bits. The
magnitude bits are in true (uncomplemented) binary for both positive and
negative numbers.
1’s Complement Form
Positive
numbers in 1’s complement form are represented the same way as the
positive sign-magnitude numbers. Negative numbers, however, are the 1’s
complements of the corresponding positive numbers. Example: The decimal number -25 is expressed as the 1’s complement of +25 (00011001) as (11100110)
2’s Complement Form
In the 2’s complement form, a negative number is the 2’s complement of the corresponding positive number
The Decimal Value of Signed Numbers
Sign-Magnitude:
Decimal
Value of positive and negative numbers in the sign-magnitude form are
determined by summing the weights in all the magnitude bit positions
where there are 1s and ignoring those positions where there are zeros.
1’s Complement:
Decimal
values of negative numbers are determined by assigning a negative value
to the weight of the sign bit, summing all the weight where there are
1s and adding 1 to the result
2’s Complement:
The weight of the sign bit in a negative number is given a negative value
Arithmetic Operations with Signed Number
In
this section we will learn how signed numbers are added, subtracted,
multiplied and divided. This section will cover only on the 2’s
complement arithmetic, because, it widely used in computers and
microprocessor-based system .
Addition
Subtraction
Multiplication
Division
The
division operation in computers is accomplished using subtraction.
Since subtraction is done with an adder, division can also be
accomplished with an adder. The result of a division is called the quotient.
Step 1:
Determine the SIGN BIT for both DIVIDEND and DIVISOR
Step 2:
Subtract
the DIVISOR from the DIVIDEND using 2’s Complement addition to get the
first partial remainder and ADD 1 to quotient. If ZERO or NEGATIVE the
division is complete.
Step 3:
Subtract the divisor from the partial remainder and ADD 1 to the quotient. If the result is POSITIVE repeat Step 2 or If ZERO or NEGATIVE the division is complete.
Hexadecimal Numbers
- Most digital systems deal with groups of bits in even powers of 2 such as 8, 16, 32, and 64 bits.
- Hexadecimal uses groups of 4 bits.
- Base 16
- 16 possible symbols
- 0-9 and A-F
- Allows for convenient handling of long binary strings.
- Convert from hex to decimal by multiplying each hex digit by its positional weight.
- Example:
- Convert from decimal to hex by using the repeated division method used for decimal to binary and decimal to octal conversion.
- Divide the decimal number by 16
- The first remainder is the LSB and the last is the MSB.
- Note, when done on a calculator a decimal remainder can be multiplied by 16 to get the result. If the remainder is greater than 9, the letters A through F are used.
- Example of hex to binary conversion:
- Hexadecimal is useful for representing long strings of bits.
- Understanding the conversion process and memorizing the 4 bit patterns for each hexadecimal digit will prove valuable later.
Binary Code Decimal (BCD)
- Binary Coded Decimal (BCD) is another way to present decimal numbers in binary form.
- BCD is widely used and combines features of both decimal and binary systems.
- Each digit is converted to a binary equivalent.
- To convert the number 87410 to BCD:
- Each decimal digit is represented using 4 bits.
- Each 4-bit group can never be greater than 9.
- Reverse the process to convert BCD to decimal.
- BCD is not a number system.
- BCD is a decimal number with each digit encoded to its binary equivalent.
- A BCD number is not the same as a straight binary number.
- The primary advantage of BCD is the relative ease of converting to and from decimal.
Alphanumeric Codes
- Represents characters and functions found on a computer keyboard.
- ASCII – American Standard Code for Information Interchange.
- Seven bit code: 27 = 128 possible code groups
- Table 2-4 lists the standard ASCII codes
- Examples of use are: to transfer information between computers, between computers and printers, and for internal storage.
